Projects include mathematics and computer algebra research for differential geometric algebras, with an interest in aerospace engineering applications. Foundations of the open source free software Grassmann.jl are based on differential geometric algebra and developed in the Julia language. Interests include applications of Grassmann.jl software to explore relationships between quantum computing, number theory, geometric flows, aeroacoustics, relativity, optics, and electrical engineering. -> Connect <-
Sponsor this at liberapay, GitHub Sponsors, Patreon, or Bandcamp; also available as part of the Tidelift Subscription.
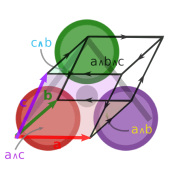
Leibniz-Grassmann-Clifford differential geometric algebra / multivector simplicial complex
The Grassmann.jl package provides tools for doing computations based on multi-linear algebra, differential geometry, and spin groups using the extended tensor algebra known as Leibniz-Grassmann-Clifford-Hestenes geometric algebra. Combinatorial products include ∧, ∨, ⋅, *, ⋆, ', ~, d, ∂ (which are the exterior, regressive, inner, and geometric products; along with the Hodge star, adjoint, reversal, differential and boundary operators). The kernelized operations are built up from composite sparse tensor products and Hodge duality, with high dimensional support for up to 62 indices using staged caching and precompilation. Code generation enables concise yet highly extensible definitions. The DirectSum.jl multivector parametric type polymorphism is based on tangent bundle vector spaces and conformal projective geometry to make the dispatch highly extensible for many applications. Additionally, the universal interoperability between different sub-algebras is enabled by AbstractTensors.jl, on which the type system is built.

Abstract tangent bundle vector space type operations at compile-time
This package is a work in progress providing the necessary tools to work with arbitrary Manifold elements specified with an encoding having optional origin, point at infinity, and tangent bundle parameter. Due to the parametric type system for the generating TensorBundle, the Julia compiler can fully preallocate and often cache values efficiently ahead of run-time. Although intended for use with the Grassmann.jl package, DirectSum can be used independently.
Tensor algebra abstract type interoperability with vector bundle parameter
The AbstractTensors package is intended for universal interoperability of the abstract TensorAlgebra type system. All TensorAlgebra{V} subtypes have type parameter V, used to store a TensorBundle value obtained from DirectSum.jl.
For example, this is mainly used in Grassmann.jl to define various SubAlgebra, TensorGraded and TensorMixed types, each with subtypes. Externalizing the abstract type helps extend the dispatch to other packages. By itself, this package does not impose any specifications or structure on the TensorAlgebra{V} subtypes and elements, aside from requiring V to be a Manifold. This means that different packages can create tensor types having a common underlying TensorBundle structure.

Dendriform dialgebra algorithms to compute Loday's arithmetic on groves of binary trees
Provides the types PBTree for planar binary trees, Grove for tree collections of constant degree, and GroveBin to compress grove data. This package defines various essential operations on planar binary trees and groves like ∪ for union; ∨ for graft; left and right for branching; ⋖, ⋗, <, >, ≤, ≥ for Tamari's partial ordering; ⊴ for between; / and \\ (i.e. over and under); and the dashv and vdash operations ⊣, ⊢, +, * for dendriform algebra.
Together these non-commutative binary operations satisfy the properties of an associative dendriform dialgebra. The structures induced by Loday's definition of the sum have the partial ordering of the associahedron known as Tamari lattice.
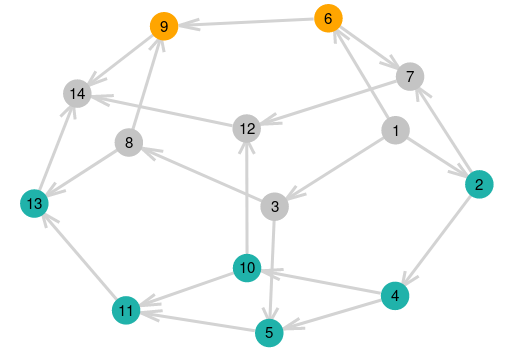
Figure: Tamari associahedron, colored to visualize noncommutative sums of [1,2] and [2,1], code: gist
View the documentation stable / latest for more features and examples.
Adaptive multistep numerical ODE solver based on Grassmann.jl element assembly
This Julia project originally started as a FORTRAN 95 project called adapode. It is possible to work with L2 projection on a mesh and partial differential equations can also be assembled with various additional methods. More general problems for finite element boundary value problems are also enabled by mesh representations imported from external sources. These methods can automatically generalize to higher dimensional manifolds and is compatible with discrete differential geometry.

Symbolic parser generator for Julia language expressions using REDUCE algebra
The premise behind Reduce.jl is based on the idea that Symbol and Expr types can be translated into computer algebra rewrite commands and then automatically parsed back into Julia ASTs, essentially extending the Julia language into a fully programable symbolic AST rewrite environment.
REDUCE is a system for general algebraic computations of interest to mathematicians, scientists and engineers. Reduce.jl is an interface for applying symbolic manipulation on Julia expressions using REDUCE's term rewrite system:
The upstream REDUCE software created by Anthony C. Hearn is maintained by collaborators on SourceForge.
This package is a heavily modifed version of Nathan Smith's Maxima.jl with many additional features.
Fatou sets in Julia (Fractals, Newton basins, Mandelbrot)
This package enables users of Julia lang to easily generate, explore, and share fractals of Julia, Mandelbrot, and Newton type. The name Fatou comes from the mathematician after whom the Fatou sets are named. Note that the Julia language is not named after the mathematician Julia after whom the Julia sets are named. This is a mere coincidence. See Explore Fatou sets & Fractals on here for detailed examples.
Toolkit for studying numerical analysis and floating point algebra round-off
This package is intended to help provide a complementary detailed analysis of polynomial rounding error estimates using newly defined local and global characteristic methods. Using automated testing of different polynomial forms, an optimal expression form can be determined. The methods used include a Simpson-Stieltjes integral method to estimate error bound discrepancy and a computationally efficient characteristic method. The conclusions of the associated research (to be published by Advances in Engineering Mathematics) indicate the SyntaxTree.exprval method can be used to select optimal numerical code for polynomial basis functions with the Reduce.jl symbolic rewrite package for the Julia language, which is based on high-level code generation and macros operating on abstract syntax trees. Due to the computational simplicity of the expression value method in comparison to the floating point error bound Simpson-Stieltjes integral estimation method, the expression value method is the demonstrably faster, more efficient, and equally reliable method for determining the optimal expression form characterization. The purpose of this package is to help with the analysis of the characteristic methods and to explore the local properties of the Wilkinson-type error bounds on the floating point pseudo-algebra for polynomials.
Typeset scattered graph data rewriter based on LaTeX nodes
This project is a prototype concept for maintaining a body of research and citations via a computational graph database. The VerTeX typeset scattered graph data rewriter is based on a new graph data format called VerTeX, which parses and generates LaTeX documents from nodes. Current specifications are concerned with how to construct new documents from theorems and definitions using graph data. This enables research collaborators to maintain databases of LaTeX nodes. The VerTeX julia package automatically parses this database of LaTeX nodes to extract citations and references. This system can also generate graph diagrams depicting the inter-relationships and dependencies of definitions, theorems, calculations, references, and results.

Theorems, Definitions, Papers, Research
Repository of chakravala/Michael's public notes. Use the DropBox link to access the most up-to-date PDF, which is automatically updated in tandem with the github repo.
